Transformations
Transformations are a class of modifiers that is used to move or distort solid object (or vectors) in space. The following types of transformations are currently available:
- Identity transformation
- Affine transformations: translation, rotation, scaling, atrafo
- Bending transformation
- Boxwarp transformation
Identity transformation
The identity transformation is the most simple transformation one can think of since it does nothing at all. However, sometimes this is exactly what one needs to do. It is available for convenience for functions that obligatorily require a transformation as an input. It has the constructor 'identity'.
Example
make identity() >> box()
Affine transformations
The class of affine transformations contains all "classic" transformations like translations, rotations and scalings (see https://en.wikipedia.org/wiki/Affine_transformation). They can generally be expressed as 3x4 matrices (see matrix calculus). Some of them have multiple constructors that are listed in the respective data type reference.
The translation transformation
The translation transformation shifts the solid or vector that it is applied on for a certain distance in one direction in space. This shift is defined as argument of type vector in its constructor. We have already shown an example of this transformation when introducing modifiers but we will repeat it here for completeness. It creates a box that is shifted by two units into the X direction:
Example
make translation( <[2.0,0.0,0.0]> ) >> box()
The rotation transformation
A rotation causes a solid to spin around a given axis. In trCAD rotations generally follow the "right hand rule" (see https://en.wikipedia.org/wiki/Right-hand_rule) that defines their movement direction. Negative angle values can be used to spin into the opposite direction.
There are two constructors available for defining a rotation. The first one is of type rotation( vector, float ). It rotates the object around the axis given as first argument for an angle given as second argument. For this constructor, the rotation axis starts at the origin of the coordinate space.
Example
box b( 1.5, 2.0, 0.0, 0.9, 0.0, 0.1 )
make rotation( <[ 0.0, 0.0, 1.0 ]>, rad( 40 ) ) >> b
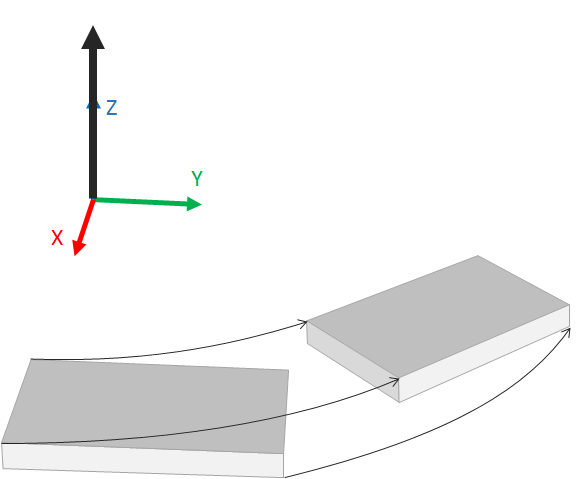
A rotation of 40 degree around the rotation axis (big black arrow) that is centered at the coordinate space origin.
The second constructor has the form rotation( vector, vector, float ). The first vector sets an onset point for the rotation axis (purple vector in the figure) while the second vector defines the rotation axis direction (big black arrow in the figure). This allows to turn any object around any arbitrary axis. The float parameter still defines the spinning angle.
Example
box b( 1.5, 2.0, 0.0, 0.9, 0.0, 0.1 )
make rotation( <[ 1.75, 0.45, 0.0 ]>, <[ 0.0, 0.0, 1.0 ]>, rad( 40 ) ) >> b
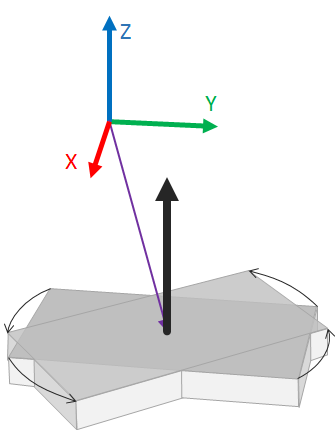
A rotation of 40 degree around the rotation axis (big black arrow) that is shifted into the object by the purple arrow.
Note
In trCAD, all angles are given in radian units (see https://en.wikipedia.org/wiki/Radian). The function rad() can be used to convert degrees into radiants.
The scaling transformation
Another simple transformation is the scaling of an object. There are four constructors for scaling: one for scaling into all directions uniformly, one for scaling unevenly into the three coordinate directions X, Y and Z and two constructors for scaling with a shifted coordinate offset. The first constructor simply takes one floating point value as an argument:
Example
make scaling( 2.0 ) >> sphere()
The second constructor accepts three floating point values, one for each direction:
Example
make scaling( 2.0, 1.0, 0.5 ) >> sphere()
The third and fourth constructors are versions of the first two that take an additional vector as first argument. This defines the center point of the scaling transformation, i.e. the point that is not shifted due to the scaling:
Example
make scaling( <[ 0.5, 0.5, 0.5 ]>, 2.0 ) >> box()
make scaling( <[ 0.5, 0.5, 0.5 ]>, 0.5, 1.0, 3.0 ) >> box()
Please note that the application of the uneven scaling constructors distorts the solid's original shape.
The atrafo transformation
The atrafo transformation allows to generate a general affine transformation directly from a matrix argument:
Example
make atrafo( <[<[ 0.5, 0.0, -0.87, 1.0 ]>,
<[ 0.0, 1.0, 0.0, 2.0 ]>,
<[ 0.87, 0.0, 0.5, 1.0 ]>]> ) >> box()
Bending transformation
The bendingtransformation operation defines a circular bending of the solids the operation is applied to around a given bending center axis. Two different constructors exist for slightly different situations. One requires to know the central point of the bending the other requires to known the radius. (For more details about the different constructors see the reference section.) In any case, the solid that gets bent should be sufficiently fine tesselated to allow a smooth surface morphing (also see the subdivision modifier).
Example
solid s = subdiv( 0.25, <[0,0,1]> ) >> box( 1, 1, 5 )
make bending( 4, <[1,0,0]>, <[0.5, 0.5, 0.0]>, <[0,0,1]> ) >> s

The bent box.
Boxwarp transformation
Sometimes a transformation is required that tilts parallel faces or edges of a solid with respect to each other. One reason may be the wish to rectify tilted faces of an object or to bring an object with parallel sides into a wedge shape. These kind of modifications can all be achieved by the boxwarp transformation. The following image shows some example changes that can be applied to an object.
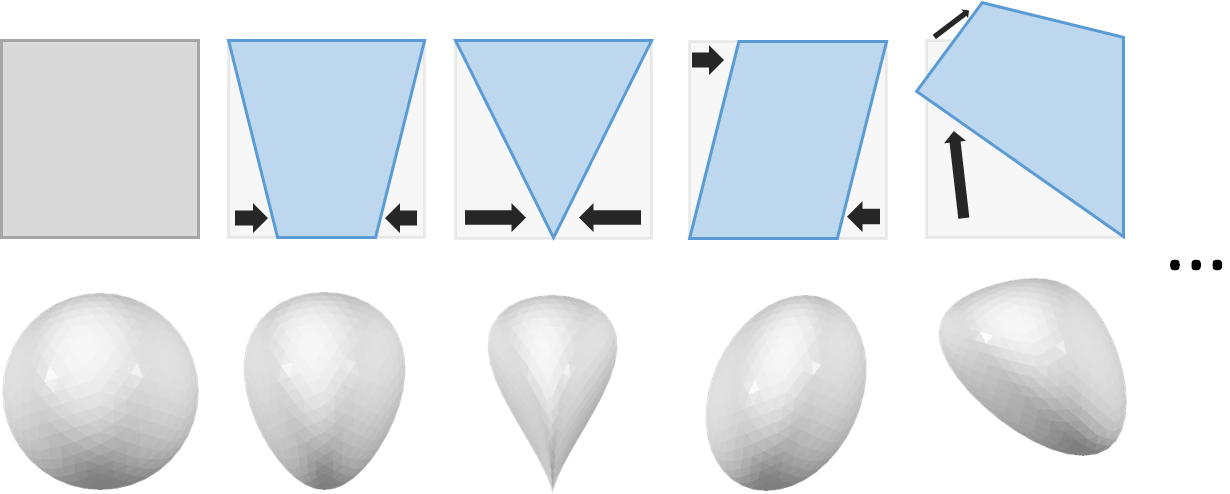
The input (left) and four possible boxwarp transformations (right). The upper row shows the input box (grey) and the transformation boxes (blue) while the lower line displays the respective deformations of a sphere.
The basic constructor of the boxwarp transformation accepts one input box (that may be a general parallelepiped, see https://en.wikipedia.org/wiki/Parallelepiped) and one transformation box. The transformation "box" can in fact be an arbitrary hexahedron (geometric shape with six faces, see https://en.wikipedia.org/wiki/Hexahedron) that is defined by its eight corner points. This makes the boxwarp transformation very general and allows many more applications than shown in the image.
The boxwarp transformation and its usage is explained in more detail in its data type reference section.
Helical transformation
The transformation along a helix spiral can be applied with the helix modifier:
Example
document.render_vis_smooth = true
make helix( <[0.5, 0.5, 1.0]>, <[0.0, 0.0, 1.0]>, PI/2.0 ) >>
subdiv( 0.05, <[0.0, 0.0, 1.0]> ) >> box()

A helical deformation of a box.