../../

Signatures

bending( vector center, vector origin, vector tangent )
bending( float radius, vector axis, vector origin, vector tangent )

Details

The bending transformation is built to bend solids in a defined way. Straight objects can be brought into circular shape by this. So it is especially suitable for planar or longitudial solids that should be bent into a cylindrical or arc form.

The geometric situation for a bending transformation can be seen in the following figure.

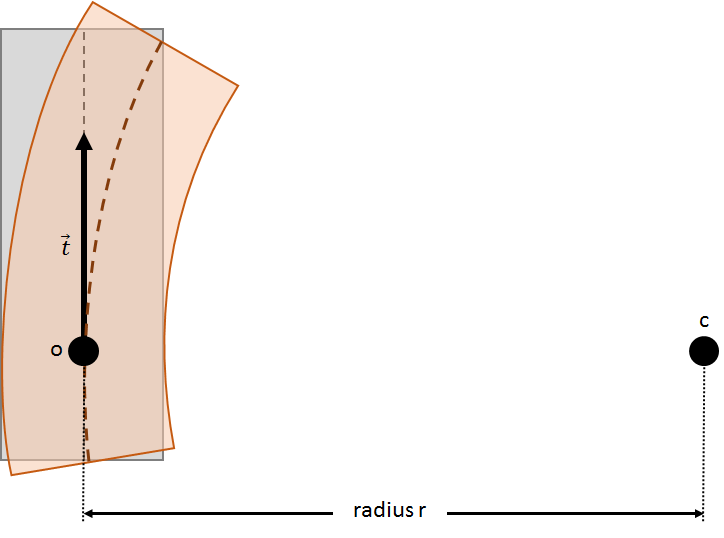
Bending transformation applied to a box.

In the figure, the grey box solid is bent around center point c, resulting in the orange box. The origin or reference point o defines one point on the isometric plane (vertical dashed line in the gray solid). This plane is defined by the fact, that the transformation of any line on it will have the same arc length as the original line. Lines on parallel planes closer to or further away from the center point get shortened or elongated by the transformation. The distance between the center point and the origin defines the radius r of the bending.

The tangent vector t is a vector in the isometric plane that is required to make the bending direction unambiguous. What cannot be seen in the image is the axis vector that sticks out of the image plane. It defines the axis the bent solid is wrapped around.

Constructor (1) is suitable whenever the center point is known. Constructor (2) may be used when the radius and the axis vector is known instead.

Note

The quality of the results of a bending transformation depends strongly on the solid's resolution in tangent vector direction. Poor resultions will lead to badly rounded, "edgy" results. This can be optimized with the subdiv modifier.

Example

 make bending( 1.0, <[ 1.0, 0.0, 0.0 ]>, <[0.0, 0.0, 0.0 ]>, <[ 0.0, 0.0, 1.0 ]>) >>
      torus( <[ 0.0, 1.0, 0.0 ]>, 1.0, 0.2 )

Casts To

string
modifier

Parameters

center

Defines the center point of the bending.

origin

Defines a point on the isometric plane. This is typically on or in the solid that is bent.

tangent

A vector in the isometric plane that defines the wrapping direction. This should be orthogonal the to axis vector.

radius

Radius of the bending when the center point is not given. The sign of the radius defines the bending direction ("to the left or to the right").

axis

Axis vector the solid is bent around. This should be orthogonal the to tangent vector.